momentum dan implus

Momentum dan Impuls - Presentation Transcript

1. MOMENTUM & IMPULS (Rumus) Momentum: Hasil kali massa benda dengan kecepatannya (besaran vektor). p : momentum benda (kg.m/s) m : massa benda (kg) v : kecepatan benda (m/s) Perubahan momentum bersudut Pada sumbu-x: Pada sumbu-y: Impuls: Perubahan momentum benda persatuan waktu (besaran vektor). I : Impuls benda (kg.m/s) m : massa benda (kg) v : kecepatan benda (m/s) p: perubahan momentum (kg.m/s) Hukum Kekekalan Momentum Jika tidak ada gaya luar yang bekerja, momentum sistem sebelum dan sesudah tumbukan sama. atau Penerapan Pada Roket FR : gaya dorong roket (N) v : kecepatan semburan gas (m/s) m : massa gas (kg) t : perubahan waktu (s) Tumbukan Lenting Sempurna Lenting Sebagian Tidak Lenting Sama Sekali e = koefisien restitusi (0 <>

Hukum kekekalan momentum

HUKUM KEKEKALAN MOMENTUM

Hukum kekekalan momentum diterapkan pada proses tumbukan semua jenis, dimana prinsip impuls mendasari proses tumbukan dua benda, yaitu I₁ = -I₂.

Jika dua benda A dan B dengan massa masing-masing M_A dan M_B serta kecepatannya masing-masing V_A dan V_B saling bertumbukan, maka :

M_A V_A + M_B V_B = M_A V_A + M_B V_B

V_A dan V_B = kecepatan benda A dan B pada saat tumbukan

V_A dan V_B = kecepatan benda A den B setelah tumbukan.

Dalam penyelesaian soal, searah vektor ke kanan dianggap positif, sedangkan ke kiri dianggap negatif.

Dua benda yang bertumbukan akan memenuhi tiga keadaan/sifat ditinjau dari keelastisannya,

a. ELASTIS SEMPURNA : e = 1

e = (- VA' - VB')/(VA - VB)

e = koefisien restitusi.
Disini berlaku hukum kokokalan energi den kokekalan momentum.

b. ELASTIS SEBAGIAN: 0 < e < 1
Disini hanya berlaku hukum kekekalan momentum.

Khusus untuk benda yang jatuh ke tanah den memantul ke atas lagi maka koefisien restitusinya adalah:

e = h'/h

h = tinggi benda mula-mula
h' = tinggi pantulan benda

C. TIDAK ELASTIS: e = 0
Setelah tumbukan, benda melakukan gerak yang sama dengan satu kecepatan v',

M_A V_A + M_B V_B = (M_A + M_B) v'

Disini hanya berlaku hukum kekekalan momentum

Contoh:

1. Sebuah bola dengan massa 0.1 kg dijatuhkan dari ketinggian 1.8 meter dan mengenai lantai, kemudian dipantulkan kembali sampai ketinggian 1.2 meter. Jika g = 10 m/det².
Tentukanlah:
a. impuls karena beret bola ketika jatuh.
b. koefisien restitusi

Jawab:

a. Selama bola jatuh ke tanah terjadi perubahan energi potensial menjadi energi kinetik.

Ep = Ek m g h = 1/2 mv2 ® v2 = 2 gh ® v = Ö2 g h impuls karena berat ketika jatuh: I = F . Dt = m . Dv = 0.1Ö2gh = 0.1 Ö(2.10.1.8) = 0.1.6 = 0,6 N det.

b. Koefisien restitusi:

e = Ö(h'/h) = Ö(1.2/1.8) = Ö(2/3)

2. Sebuah bola massa 0.2 kg dipukul pada waktu sedang bergerak dengan kecepatan 30 m/det. Setelah meninggalkan pemukul, bola bergerak dengan kecepatan 40 m/det berlawanan arah semula. Hitung impuls pada tumbukan tersebut !

Jawab:

Impuls = F . t = m (v₂ - v₁)

= 0.2 (-40 - 30)

= -14 N det

Tanda berarti negatif arah datangnya berlawanan dengan arah datangnya bola.

3. Sebuah peluru yang massanya M₁ mengenai sebuah ayunan balistik yang massanya M₂. Ternyata pusat massa ayunan naik setinggi h, sedangkan peluru tertinggal di dalam ayunan. Jika g = percepatan gravitasi, hitunglah kecepatan peluru pada saat ditembakkan !

Jawab:

Penyelesaian soal ini kita bagi dalam dua tahap, yaitu:

1. Gerak A - B.

Tumbukan peluru dengan ayunan adalah tidak elastis jadi kekekalan momentumnya: M1VA + M2VB = (M1 + M2) V M1VA + 0 = (M1 + M2) V VA = [(M1 + M2)/M1] . v

2. Gerak B - C.
Setelah tumbukan, peluru dengan ayunan naik setinggi h, sehingga dapat diterapkan kekekalan energi:

E_MB = E_MC

E_pB + E_kB = E_pC + E_kC

0 + 1/2 (M₁ + M₂) v² = (M₁ + M₂) gh + 0

Jadi kecepatan peluru: V_A = [(M₁ + M₂)/M1] . Ö(2 gh)

d. ELASTISITAS KHUSUS DALAM ZAT PADAT

Zat adalah suatu materi yang sifat-sifatnya sama di seluruh bagian, dengan kata lain, massa terdistribusi secara merata. Jika suatu bahan (materi) berupa zat padat mendapat beban luar, seperti tarikan, lenturan, puntiran, tekanan, maka bahan tersebut akan mengalami perubahan bentuk tergantung pada jenis bahan dan besarnya pembebanan. Benda yang mampu kembali ke bentuk semula, setelah diberikan pembebanan disebut benda bersifat elastis.

Suatu benda mempunyai batas elastis. Bila batas elastis ini dilampaui maka benda akan mengalami perubahan bentuk tetap, disebut juga benda bersifat plastis.

momentum

Dalam mekanika klasik, momentum (dilambangkan dengan p) didefinisikan sebagai hasil perkalian dari massa dan kecepatan, sehingga menghasilkan vektor.

Rumus yang biasa digunakan untuk menghitung nilai momentum benda yaitu:

Dimana P adalah momentum, m adalah massa benda, dan v adalah kecepatan.

Momentum adalah besaran vektor. Momentum sebuah partikel dapat dipandang sebagai ukuran kesulitan untuk mendiamkan benda. Sebagai contoh, sebuah truk berat mempunyai momentum yang lebih besar dibandingkan mobil yang ringan yang bergerak dengan kelajuan yang sama. Gaya yang lebih besar dibutuhkan untuk menghentikan truk tersebut dibandingkan dengan mobil yang ringan dalam waktu tertentu. (Besaran mv kadang-kadang dinyatakan sebagai momentum linier partikel untuk membedakannya dari momentum angular).

penerapan hukum kekekalan energi mekanik

Hukum Kekekalan Energi Mekanik pada Gerak Jatuh Bebas

Suatu contoh sederhana dari Hukum Kekekalan Energi Mekanik adalah ketika sebuah benda melakukan Gerak Jatuh Bangun, eh… Gerak Jatuh Bebas (GJB).

Misalnya kita tinjau sebuah batu yang dijatuhkan dari ketinggian tertentu. Pada analisis mengenai Gerak Jatuh Bebas, hambatan udara diabaikan, sehingga pada batu hanya bekerja gaya berat (gaya berat merupakan gaya gravitasi yang bekerja pada benda, di mana arahnya selalu tegak lurus menuju permukaan bumi).

Ketika batu berada pada ketinggian tertentu dari permukaan tanah dan batu masih dalam keadaan diam, batu tersebut memiliki Energi Potensial sebesar EP = mgh. m adalah massa batu, g adalah percepatan gravitasi dan h adalah kedudukan batu dari permukaan tanah (kita gunakan tanah sebagai titik acuan). ketika berada di atas permukaan tanah sejauh h (h = high = tinggi), Energi Kinetik (EK) batu = 0. mengapa nol ? batu masih dalam keadaan diam, sehingga kecepatannya 0. EK = ½ mv², karena v = 0 maka EK juga bernilai nol alias tidak ada Energi Kinetik. Total Energi Mekanik = Energi Potensial.

EM = EP + EK

EM = EP + 0

EM = EP

Sambil lihat gambar di bawah ya….

Apabila batu kita lepaskan, batu akan jatuh ke bawah akibat gaya tarik gravitasi yang bekerja pada batu tersebut. Semakin ke bawah, EP batu semakin berkurang karena kedudukan batu semakin dekat dengan permukaan tanah (h makin kecil). Ketika batu bergerak ke bawah, Energi Kinetik batu bertambah. Ketika bergerak, batu mempunyai kecepatan. Karena besar percepatan gravitasi tetap (g = 9,8 m/s²), kecepatan batu bertambah secara teratur. Makin lama makin cepat. Akibatnya Energi Kinetik batu juga semakin besar. Nah, Energi Potensial batu malah semakin kecil karena semakin ke bawah ketinggian batu makin berkurang. Jadi sejak batu dijatuhkan, EP batu berkurang dan EK batu bertambah. Jumlah total Energi Mekanik (Energi Kinetik + Energi Potensial = Energi Mekanik) bernilai tetap alias kekal bin tidak berubah. Yang terjadi hanya perubahan Energi Potensial menjadi Energi Kinetik.

Ketika batu mencapai setengah dari jarak tempuh total, besar EP = EK. Jadi pada posisi ini, setengah dari Energi Mekanik = EP dan setengah dari Energi Mekanik = EK. Ketika batu mencium tanah, batu, pasir dan debu dengan kecepatan tertentu, EP batu lenyap tak berbekas karena h = 0, sedangkan EK bernilai maksimum. Pada posisi ini, total Energi Mekanik = Energi Kinetik. Gampang aja…. dirimu bisa menjelaskan dengan mudah apabila telah memahami konsep Gerak Jatuh Bebas, Energi Kinetik, Energi potensial dan Hukum Kekekalan Energi Mekanik. Semua materi itu sudah ada di blog ini…. jika belum memahami konsep-konsep tersebut dengan baik dan benar, sangat disarankan agar dipelajari kembali hingga benar-benar ngerti….

Hukum Kekekalan Energi Mekanik pada Gerak parabola

Hukum kekekalan energi mekanik juga berlaku ketika benda melakukan gerakan parabola.

Ketika benda hendak bergerak (benda masih diam), Energi Mekanik yang dimiliki benda sama dengan nol. Ketika diberikan kecepatan awal sehingga benda melakukan gerakan parabola, EK bernilai maksimum (kecepatan benda besar) sedangakn EP bernilai minimum (jarak vertikal alias h kecil). Semakin ke atas, kecepatan benda makin berkurang sehingga EK makin kecil, tetapi EP makin besar karena kedudukan benda makin tinggi dari permukaan tanah. Ketika mencapai titik tertinggi, EP bernilai maksimum (h maksimum), sedangkan EK bernilai minimum (hanya ada komponen kecepatan pada arah vertikal).Ketika kembali ke permukaan tanah, EP makin berkurang sedangkan EK makin besar dan EK bernilai maksimum ketika benda menyentuh tanah. Jumlah energi mekanik selama benda bergerak bernilai tetap, hanya selama gerakan terjadi perubahan energi kinetik menjadi energi potensial (ketika benda bergerak ke atas) dan sebaliknya ketika benda bergerak ke bawah terjadi perubahan energi potensial menjadi energi kinetik.

Hukum Kekekalan Energi Mekanik pada Gerak Harmonik Sederhana

Terdapat dua jenis gerakan yang merupakan Gerak Harmonik Sederhana, yakni ayunan sederhana dan getaran pegas. Jika dirimu belum paham apa itu Gerak Harmonik Sederhana, silahkan pelajari materi Gerak Harmonik Sederhana yang telah dimuat pada blog ini. Silahkan meluncur ke TKP…..

Sekarang mari kita tinjau Hukum Kekekalan Energi Mekanik pada ayunan sederhana.

Untuk menggerakan benda yang diikatkan pada ujung tali, benda tersebut kita tarik ke kanan hingga mencapai titik A. Ketika benda belum dilepaskan (benda masih diam), Energi Potensial benda bernilai maksimum, sedangkan EK = 0 (EK = 0 karena benda diam ). Pada posisi ini, EM = EP. Ingat bahwa pada benda bekerja gaya berat w = mg. Karena benda diikatkan pada tali, maka ketika benda dilepaskan, gaya gravitasi sebesar w = mg cos teta menggerakan benda menuju posisi setimbang (titik B). Ketika benda bergerak dari titik A, EP menjadi berkurang karena h makin kecil. Sebaliknya EK benda bertambah karena benda telah bergerak. Pada saat benda mencapai posisi B, kecepatan benda bernilai maksimum, sehingga pada titik B Energi Kinetik menjadi bernilai maksimum sedangkan EP bernilai minimum. Karena pada titik B kecepatan benda maksimum, maka benda bergerak terus ke titik C. Semakin mendekati titik C, kecepatan benda makin berkurang sedangkan h makin besar. Kecepatan berkurang akibat adanya gaya berat benda sebesar w = mg cos teta yang menarik benda kembali ke posisi setimbangnya di titik B. Ketika tepat berada di titik C, benda berhenti sesaat sehingga v = 0. karena v = 0 maka EK = 0. pada posisi ini, EP bernilai maksimum karena h bernilai maksimum. EM pada titik C = EP. Akibat tarika gaya berat sebesar w = mg cos teta, maka benda bergerak kembali menuju titik B. Semakin mendekati titik B, kecepatan gerak benda makin besar, karenanya EK semakin bertambah dan bernilai maksimum pada saat benda tepat berada pada titik B. Semikian seterusnya, selalu terjadi perubahan antara EK dan EP. Total Energi Mekanik bernilai tetap (EM =EP + EK).

Hukum Kekekalan Energi Mekanik (HKEM) pada Getaran Pegas

Getaran pegas terdiri dari dua jenis, yakni getaran pegas yang diletakan secara horisontal dan getaran pegas yang digantungkan secara vertikal. Sebelum kita membahas satu persatu, perlu anda ketahui bahwa Energi Potensial tidak mempunyai suatu persamaan umum yang mewakili semua jenis gerakan, seperti EK. Persamaan EK tersebut bersifat umum untuk semua jenis gerakan, sedangkan Energi potensial tidak. Persamaan EP = mgh merupakan persamaan EP gravitasi, sedangkan EP elastis (untuk pegas dkk), persamaan EP-nya adalah :

Silahkan pelajari materi Energi Potensial dan Energi Kinetik yang telah dimuat di blog ini agar dirimu semakin paham.

Hubungan usaha dengan perubahan energi kinetik

Energi Kinetik

Setiap benda yang bergerak memiliki energi. Ketapel yang ditarik lalu dilepaskan sehingga batu yang berada di dalam ketapel meluncur dengan kecepatan tertentu. Batu yang bergerak tersebut memiliki energi. Jika diarahkan pada ayam tetangga maka kemungkinan besar ayam tersebut lemas tak berdaya akibat dihajar batu. Pada contoh ini batu melakukan kerja pada ayam Kendaraan beroda yang bergerak dengan laju tertentu di jalan raya juga memiliki energi kinetik. Ketika dua buah kendaraan yang sedang bergerak saling bertabrakan, maka bisa dipastikan kendaraan akan digiring ke bengkel untuk diperbaiki. Kerusakan akibat tabrakan terjadi karena kedua mobil yang pada mulanya bergerak melakukan usaha / kerja satu terhadap lainnya. Ketika tukang bangunan memukul paku menggunakan martil, martil yang digerakan tukang bangunan melakukan kerja pada paku.

Setiap benda yang bergerak memberikan gaya pada benda lain dan memindahkannya sejauh jarak tertentu. Benda yang bergerak memiliki kemampuan untuk melakukan kerja, karenanya dapat dikatakan memiliki energi. Energi pada benda yang bergerak disebut energi kinetik. Kata kinetik berasal dari bahasa yunani, kinetikos, yang artinya “gerak”. ketika benda bergerak, benda pasti memiliki kecepatan. Dengan demikian, kita dapat menyimpulkan bahwa energi kinetik merupakan energi yang dimiliki benda karena gerakannya atau kecepatannya.

Sekarang mari kita turunkan persamaan Energi Kinetik.

Untuk menurunkan persamaan energi kinetik, bayangkanlah sebuah benda bermassa m sedang bergerak pada lintasan lurus dengan laju awal v_o.

Agar benda dipercepat beraturan sampai bergerak dengan laju v maka pada benda tersebut harus diberikan gaya total yang konstan dan searah dengan arah gerak benda sejauh s. Untuk itu dilakukan usaha alias kerja pada benda tersebut sebesar W = F s. Besar gaya F = m a.

Karena benda memiliki laju awal v_o, laju akhir v_t dan bergerak sejauh s, maka untuk menghitung nilai percepatan a, kita menggunakan persamaan vt² = vo² + 2as.

Kita subtitusikan nilai percepatan a ke dalam persamaan gaya F = m a, untuk menentukan besar usaha :

Persamaan ini menjelaskan usaha total yang dikerjakan pada benda. Karena W = EK maka kita dapat menyimpulkan bahwa besar energi kinetik translasi pada benda tersebut adalah :

W = EK = ½ mv² —– persamaan 2

Persamaan 1 di atas dapat kita tulis kembali menjadi :

Persamaan 3 menyatakan bahwa usaha total yang bekerja pada sebuah benda sama dengan perubahan energi kinetiknya. Pernyataan ini merupakan prinsip usaha-energi. Prinsip usaha-energi berlaku jika W adalah usaha total yang dilakukan oleh setiap gaya yang bekerja pada benda. Jika usaha positif (W) bekerja pada suatu benda, maka energi kinetiknya bertambah sesuai dengan besar usaha positif tersebut (W). Jika usaha (W) yang dilakukan pada benda bernilai negatif, maka energi kinetik benda tersebut berkurang sebesar W. Dapat dikatakan bahwa gaya total yang diberikan pada benda di mana arahnya berlawanan dengan arah gerak benda, maka gaya total tersebut mengurangi laju dan energi kinetik benda. Jika besar usaha total yang dilakukan pada benda adalah nol, maka besar energi kinetik benda tetap (laju benda konstan).

Hubungan usaha dengan perubahan energi potensial

Energi Potensial

Energi potensial merupakan energi yang dihubungkan dengan gaya-gaya yang bergantung pada posisi atau wujud benda dan lingkungannya. Banyak sekali contoh energi potensial dalam kehidupan kita. Karet ketapel yang kita regangkan memiliki energi potensial. Karet ketapel dapat melontarkan batu karena adanya energi potensial pada karet yang diregangkan. Demikian juga busur yang ditarik oleh pemanah dapat menggerakan anak panah, karena terdapat energi potensial pada busur yang diregangkan. Contoh lain adaah pegas yang ditekan atau diregangkan. Energi potensial pada tiga contoh ini disebut senergi potensial elastik. Energi kimia pada makanan yang kita makan atau energi kimia pada bahan bakar juga termasuk energi potensial. Ketika makanan di makan atau bahan bakar mengalami pembakaran, baru energi kimia yang terdapat pada makanan atau bahan bakar tersebut dapat dimanfaatkan. Energi magnet juga termasuk energi potensial. Ketika kita memegang sesuatu yang terbuat dari besi di dekat magnet, pada benda tersebut sebenarnya bekerja energi potensial magnet. Ketika kita melepaskan benda yang kita pegang (paku, misalnya), dalam waktu singkat paku tersebut bergerak menuju magnet dan menempel pada magnet. Perlu dipahami bahwa paku memiliki energi potensial magnet ketika berada jarak tertentu dari magnet; ketika menempel pada magnet, energi potensial bernilai nol.

Energi Potensial Gravitasi

Contoh yang paling umum dari energi potensial adalah energi potensial gravitasi. Buah mangga yang lezat dan ranum memiliki energi potensial gravitasi ketika sedang menggelayut pada tangkainya. Demikian juga ketika anda berada pada ketinggian tertentu dari permukaan tanah (misalnya di atap rumah atau di dalam pesawat). Energi potensial gravitasi dimiliki benda karena posisi relatifnya terhadap bumi. Setiap benda yang memiliki energi potensial gravitasi dapat melakukan kerja apabila benda tersebut bergerak menuju permukaan bumi (misalnya buah mangga jatuh dari pohon). Untuk memudahkan pemahamanmu, lakukan percobaan sederhana berikut ini. Pancangkan sebuah paku di tanah. Angkatlah sebuah batu yang ukurannya agak besar dan jatuhkan batu tegak lurus pada paku tersebut. Amati bahwa paku tersebut terpancang semakin dalam akibat usaha alias kerja yang dilakukan oleh batu yang anda jatuhkan.

ENERGI

Segala sesuatu yang kita lakukan dalam kehidupan sehari-hari membutuhkan energi. Untuk bertahan hidup kita membutuhkan energi yang diperoleh dari makanan. Setiap kendaraan membutuhkan energi untuk bergerak dan energi itu diperoleh dari bahan bakar. Hewan juga membutuhkan energi untuk hidup, sebagaimana manusia dan tumbuhan.

Energi merupakan salah satu konsep yang paling penting dalam fisika. Konsep yang sangat erat kaitannya dengan usaha adalah konsep energi. Secara sederhana, energi merupakan kemampuan melakukan usaha. Definisi yang sederhana ini sebenarnya kurang tepat atau kurang valid untuk beberapa jenis energi (misalnya energi panas atau energi cahaya tidak dapat melakukan kerja). Definisi tersebut hanya bersifat umum. Secara umum, tanpa energi kita tidak dapat melakukan kerja. Sebagai contoh, jika kita mendorong sepeda motor yang mogok, usaha alias kerja yang kita lakukan menggerakan sepeda motor tersebut. Pada saat yang sama, energi kimia dalam tubuh kita menjadi berkurang, karena sebagian energi kimia dalam tubuh berubah menjadi energi kinetik sepeda motor. Usaha dilakukan ketika energi dipindahkan dari satu benda ke benda lain. Contoh ini juga menjelaskan salah satu konsep penting dalam sains, yakni kekekalan energi. Jumlah total energi pada sistem dan lingkungan bersifat kekal alias tetap. Energi tidak pernah hilang, tetapi hanya dapat berubah bentuk dari satu bentuk energi menjadi bentuk energi lain. Mengenai Hukum Kekekalan Energi akan kita kupas tuntas dalam pokok bahasan tersendiri. (tuh ada linknya di bawah)…..

Dalam kehidupan sehari-hari terdapat banyak jenis energi. Energi kimia pada bahan bakar membantu kita menggerakan kendaraan, demikian juga energi kimia pada makanan membantu makhluk hidup bertahan hidup dan melakukan kerja. Dengan adanya energi listrik, kita bisa menonton TV atau menyalakan komputer sehingga bisa bermain game sepuasnya. Ini hanya beberapa contoh dari sekian banyak jenis energi dalam kehidupan kita. Misalnya ketika kita menyalakan lampu neon, energi listrik berubah menjadi energi cahaya. Energi listrik juga bisa berubah menjadi energi panas (setrika listrik), energi gerak (kipas angin) dan sebagainya. Banyak sekali contoh dalam kehidupan kita, dirimu bisa memikirkan contoh lainnya. Secara umum, energi bermanfaat bagi kita ketika energi mengalami perubahan bentuk, misalnya energi listrik berubah menjadi energi gerak (kipas angin), atau energi kimia berubah menjadi energi gerak (mesin kendaraan).

Usaha dan Energi

USAHA

Usaha alias Kerja yang dilambangkan dengan huruf W (Work-bahasa inggris), digambarkan sebagai sesuatu yang dihasilkan oleh Gaya (F) ketika Gaya bekerja pada benda hingga benda bergerak dalam jarak tertentu. Hal yang paling sederhana adalah apabila Gaya (F) bernilai konstan (baik besar maupun arahnya) dan benda yang dikenai Gaya bergerak pada lintasan lurus dan searah dengan arah Gaya tersebut.

Secara matematis, usaha yang dilakukan oleh gaya yang konstan didefinisikan sebagai hasil kali perpindahan dengan gaya yang searah dengan perpindahan.

Persamaan matematisnya adalah :

W = Fs cos 0 = Fs (1) = Fs

W adalah usaha alias kerja, F adalah besar gaya yang searah dengan perpindahan dan s adalah besar perpindahan.

Apabila gaya konstan tidak searah dengan perpindahan, sebagaimana tampak pada gambar di bawah, maka usaha yang dilakukan oleh gaya pada benda didefinisikan sebagai perkalian antara perpindahan dengan komponen gaya yang searah dengan perpindahan. Komponen gaya yang searah dengan perpindahan adalah F cos teta

Secara matematis dirumuskan sebagai berikut :

Hasil perkalian antara besar gaya (F) dan besar perpindahan (s) di atas merupakan bentuk perkalian titik atau perkalian skalar. Karenanya usaha masuk dalam kategori besaran skalar. Pelajari lagi perkalian vektor dan skalar kalau dirimu bingun… Persamaan di atas bisa ditulis dalam bentuk seperti ini :

Satuan Usaha dalam Sistem Internasional (SI) adalah newton-meter. Satuan newton-meter juga biasa disebut Joule ( 1 Joule = 1 N.m). menggunakan sistem CGS (Centimeter Gram Sekon), satuan usaha disebut erg. 1 erg = 1 dyne.cm. Dalam sistem British, usaha diukur dalam foot-pound (kaki-pon). 1 Joule = 10⁷ erg = 0,7376 ft.lb.

Perlu anda pahami dengan baik bahwa sebuah gaya melakukan usaha apabila benda yang dikenai gaya mengalami perpindahan. Jika benda tidak berpindah tempat maka gaya tidak melakukan usaha. Agar memudahkan pemahaman anda, bayangkanlah anda sedang menenteng buku sambil diam di tempat. Walaupun anda memberikan gaya pada buku tersebut, sebenarnya anda tidak melakukan usaha karena buku tidak melakukan perpindahan. Ketika anda menenteng atau menjinjing buku sambil berjalan lurus ke depan, ke belakang atau ke samping, anda juga tidak melakukan usaha pada buku. Pada saat menenteng buku atau menjinjing tas, arah gaya yang diberikan ke atas, tegak lurus dengan arah perpindahan. Karena tegak lurus maka sudut yang dibentuk adalah 90^o. Cos 90^o = 0, karenanya berdasarkan persamaan di atas, nilai usaha sama dengan nol. Contoh lain adalah ketika dirimu mendorong tembok sampai puyeng… jika tembok tidak berpindah tempat maka walaupun anda mendorong sampai banjir keringat, anda tidak melakukan usaha. Kita dapat menyimpulkan bahwa sebuah gaya tidak melakukan usaha apabila gaya tidak menghasilkan perpindahan dan arah gaya tegak lurus dengan arah perpindahan.

Percepatan Getar

Persamaan percepatan didapat dari turunan pertama persamaan kecepatan dari suatu gerak harmonik.

a_y=dy/dt

=-(4π²)/T² A sin⁡ (2π/T) t,tanpa posisi awal

=- (4π²)/T² A sin⁡ ( 2π/T) t+ θ₀₎,dengan posisi awal θ₀

'Persamaan tersebut dapat pula disederhanakan menjad'i

a_y= (-2π/T)y= - ω y

'

Tanda minus ( - ) menyatakan arah dari percepatan berlawanan dengan arah simpangan, Kedua persamaan diatas (persamaan kecepatan dan percepatan) tidak kita turunkan disini ,
Energy pada gerak harmonic sederhana terdiri atas energy potensial dan energy kinetik. Dengan demikian energi total dari gerak harmonik sederhana merupakan jumlah dari energi potensial dan energy kinetiknya.

Ep = 1/2 k y² dengan k= (4π² m)/T² dan y=A sin⁡θ

Ek = 1/2 mv_y² dengan v_y= 2π/T A cos⁡θ

E_T =Ep+Ek

E_T = 1/2 k A²

'Keterangan:
A = amplitude (m)
T = Periode (s)
K = konstanta pegas (N/m)
Contoh soal:
Sebuah partikel melakukan gerak harmonic sederhana dengan frekuensi 5 Hz. Jika simpangan yang dapat ditempuh partikel itu pada saat t = 2 sekon adalah 20 cm, tentukanlah percepatan getar partikel pada saat itu!
Penyelesaian
'Diketahui:
f = 5 Hz
t = 2 sekon
y = 20 cm
a = - ω².y=(2πf)².y= - (2.π.5)².20
= -2000 πcm/s² = - 20 π m/s²

Simpangan getaran

I. GETARAN1. Pengertian Getaran
Getaran adalah gerak bolak-balik atau gerak periodik disekitar titik tertentu secara periodik.

Gerak Periodik adalah suatu getaran atau gerakan yang dilakukan benda secara bolak-balik melalui jalan tertentu yang kembali lagi ke tiap kedudukan dan kecepatan setelah selang waktu tertentu.

Simpangan adalah jarak antara kedudukan benda yang bergetar pada suatu saat sampai kembali pada kedudukan seimbangnya.

Amplitudo adalah simpangan maksimum yang dilakukan pada peristiwa getaran.

Perioda adalah waktu yang diperlukan untuk melakukan satu kali getaran penuh.

Frekuensi adalah banyaknya getaran penuh yang dapat dilakukan dalam waktu satu detik.

2. Ayunan Sederhana
Ayunan sederhana atau disebut bandul melakukan gerakan bolak balik sepanjang busur AB.
Waktu yang diperlukan oleh benda untuk bergerak dari titik A ke titik A lagi disebut Satu Perioda.
Sedangkan banyaknya getaran atau gerak bolak-balik yang dapat dilakukan dalam waktu satu detik disebut Frekuensi.
Frekuensi yang dihasilkan bandul disebut Frekuensi Alamiah.
Frekuensi Alamiah adalah frekuensi yang ditimbulkan dari ayunan tanpa adanya pengaruh luar.

Gb. Gaya pd Ayunan Sederhana

Untuk Mengetahui besarnya gaya yang mempengaruhi gerak ayunan dapat digunakan persamaan berikut ini :



Dimana :

F : Gaya (N)
m : Massa benda (Kg)
g : Percepatan gravitasi (ms^-2)
θ : Sudut simpangan (…^o)
l : Panjang tali (m)
x : Simpangan getar (m)

Simpangan getar (A) dapat diketahui besarnya melalui persamaan sebagai berikut :

Dimana :

A : Simpangan getar (Amplitudo) (m)
θ : Sudut deviasi (…^o)
l : Panjang tali (m)

Sedangkan perioda getaran pada ayunan sederhana dapat diketahui melalui persamaan sebagai berikut :

Dimana :

T : Perioda getaran (S)
phi : 3,14 ( 22/7)
l : Panjang tali (m)
g : Percepatan gravitasi (ms^-2)

Frekuensi getaran dapat dicari dengan menggunakan persamaan sebagai berikut :

Dimana :
f : Frekuensi getaran (Hz)
phi : 3,14 (22/7)
g : Percepatan gravitasi (ms^-2)
l : Panjang tali (m)
T : Periode getaran (s)

SOAL

Sebuah bandul memiliki massa 100 gr dengan panjang tali 40 cm. Apabila percepatan gravitasi bumi 10 ms-2 dan bandul tersebut diberi sudut simpangan sebesar 10o. Tentukanlah amplitudo getaran dan gaya pada saat simpangan maksimum serta perioda getarannya!

3. Pegas

Getaran pada pegas memiliki frekuensi alamiah sendiri. Waktu yang diperlukan oleh benda untuk bergerak dari titik A kembali lagi ke titik A lagi disebut satu perioda dimana besarnya tergantung pada massa beban dan konstanta gaya pegas.

Besarnya gaya yang menyebabkan getaran dapat di ketahui melalui persamaan sebagai berikut :

Dimana :

F : Gaya (N)

k : Konstanta gaya pegas (N/m)

x : Simpangan (m)

Konstanta gaya pegas dapat diketahui melalui persamaan sebagai berikut :

Dimana :
k : Konstanta pegas (N/m)
m : Massa benda (Kg)
ω : Kecepatan sudut dari gerak pegas

Sedangkan untuk mengetahui besarnya frekuensi getarannya melalui persamaan sebagai berikut :
Dimana :
f : Frekuensi getaran (Hz)
phi: 3,14 (22/7)
k : Konstanta gaya pegas
m : Massa beban

Dan besarnya perioda getar dapat diketahui melalui persamaan sebagai berikut :

Dimana :

T : Perioda getar
phi : 3,14 (22/7)
m : Massa beban
k : Konstanta gaya pegas

SOAL

Sebuah pegas dengan tetapan gaya pegas sebesar 50 N/m dengan massa beban sebesar 50 gr. Dari keadaan setimbangannya pegas ditarik dengan gaya 2N. Tentukanlah simpangan maksimu, periode getarannya dan frekuensi getarannya


4. Hukum Kekekalan Energi Mekanik Pada Getaran

Besarnya energi mekanik dari suatu benda yang bergerak secara periodik adalah tetap.

Energi mekanik adalah jumlah dari energi kinetik dan energi potensial.

Di dalam setiap getaran energi potensial dan energi kinetik besarnya selalu berubah-ubah tetapi memiliki jumlah yang tetap.

Besarnya energi potensial dari benda yang bergetar secara periodik dapat diketahui melalui persamaan sebagai berikut :
Dimana :
Ep : Energi Potensial
k : Konstanta gaya pegas
y : Simapangan getaran

Gerak harmonik sederhana

Gerak Harmonik Sederhana (GHS) adalah gerak periodik dengan lintasan yang ditempuh selalu sama (tetap). Gerak Harmonik Sederhana mempunyai persamaan gerak dalam bentuk sinusoidal dan digunakan untuk menganalisis suatu gerak periodik tertentu. Gerak periodik adalah gerak berulang atau berosilasi melalui titik setimbang dalam interval waktu tetap. Gerak Harmonik Sederhana dapat dibedakan menjadi 2 bagian, yaitu :

• Gerak Harmonik Sederhana (GHS) Linier, misalnya penghisap dalam silinder gas, gerak osilasi air raksa / air dalam pipa U, gerak horizontal / vertikal dari pegas, dan sebagainya.
• Gerak Harmonik Sederhana (GHS) Angular, misalnya gerak bandul/ bandul fisis, osilasi ayunan torsi, dan sebagainya.

Beberapa Contoh Gerak Harmonik

• Gerak harmonik pada bandul: Sebuah bandul adalah massa (m) yang digantungkan pada salah satu ujung tali dengan panjang l dan membuat simpangan dengan sudut kecil. Gaya yang menyebabkan bandul ke posisi kesetimbangan dinamakan gaya pemulih yaitu dan panjang busur adalah Kesetimbangan gayanya. Bila amplitudo getaran tidak kecil namun tidak harmonik sederhana sehingga periode mengalami ketergantungan pada amplitudo dan dinyatakan dalam amplitudo sudut
• Gerak harmonik pada pegas: Sistem pegas adalah sebuah pegas dengan konstanta pegas (k) dan diberi massa pada ujungnya dan diberi simpangan sehingga membentuk gerak harmonik. Gaya yang berpengaruh pada sistem pegas adalah gaya Hooke,

Gerak harmonik sederhana

Modulus Young dapat diartikan secara sederhana, yaitu adalah hubungan besaran tegangan tarik dan regangan tarik. Lebih jelasnya adalah perbandingan antara tegangan tarik dan regangan tarik. Modulus Young sangat penting dalam ilmu fisika karena setelah mempelajarinya, kita bisa menggunakannya untuk menentukan nilai kelastisan dari sebuah benda.
Karena dirasa penting bagi mahasiswa untuk mengetahui dan menguasainya, dilakukanlah sebuah praktikum untuk memperdalam materi fisika tentang Modulus Young.
Selanjutnya, untuk melengkapi praktikum tersebut, disusunlah laporan praktikum itu. Isi dari laporan ini tak lain adalah tinjauan pustaka yang berisi teori-teori Modulus Young, tujuan praktikum, hasil-hasil pengamatan dan pembahasan hal-hal yang telkah terjadi dalam praktikum. Tujuan lain dari laporan ini adalah memenuhi salah satu tugas dari mata kuliah fisika dasar.

1.Keelastisan
Jika anda menarik sebuah pegas untuk melatih otot dada, maka pegas akan berubah bentuk, yaitu akan semakin panjang. Tetapi, bila anda melepaskan tangan anda, pegas akan segera kembali ke betuk semula. Atau contoh lain adalah pada katepel yang terbuat dari karet.
Pegas dan karet dalam hal inimerupakan benda dengan sifat elastis. Sifat elastis atau elastisitas adalah kemampuan suatu benda untuk kembali ke bentuk awalnya segera setelah gaya luar yang diberikan kepada benda itu dihilangkan.
Sedangkan benda yang tidak elastis adalah benda yang tidak kembali ke bentuk awalnya saat gaya dilepaskan, misalnya saja pada tanah liat. Bila anda menekan segumpal tanah liat, bentuknya akan berubah, tetapi saat gaya dilepaskan dari benda, tanah liat tidak kembali ke bentuk awalnya.

2.Tegangan
Tegangan didefinisikan sebagai hasil bagi antara gaya tarik F yang dialami kawat dengan luas penampangnya (A) atau bisa juga didefinisikan sebaghai gaya per satuan luas. Tegangan dirumuskan oleh:


Tegangan merupakan sebuah besaran skalar dan memiliki satuan N/m² atau Pascal (Pa).

3.Regangan
Regangan didefinisikan sebagai hasil bagi antara pertambahan panjang ∆L dengan panjang awalnya L. Atau perbandingan perubahan panjang dengan panjang awal. Regangan dirumuskan oleh:


Karena pertambahan panjang ∆L dan panjang awal L adalah besaran yang sama, maka regangan e tidak memiliki satuan atau dimensi.

Elasitatas

4.Modulus Elastis
Kebanyakan benda adlah elastis sampai ke suatu gaya yang tertentu besarnya, dinamakan batas elastis. Jika gaya yang dikerjakan/diberikan pada benda lebih kecil dari batas elastisnya, benda akan kembali ke bentuk semula jika gaya dihilangkan. Tetapi jika gaya yang diberikan melampui batas elastis, benda tak akian kembali ke bentuk semula, melainkan secara permanen berubah bentuk.









Grafik diatas menunjukkan grafik tegangan terhadap regangan ketika sebuah kawat diberi gaya hingga kawat tersebut patah.
Dari O ke B, deformasi kawat adalah elastis. Ini berarti jika tegangan dihilangkan, kawat akan kembali ke bentuk semula. Dalam daerah elastis ini, terdapat daerah yang memiliki garis linier/garis lurus, yaitu OA. Dari O sampai A ini berlaku hukum Hooke, dan titik A disebut sebagai batas hukum Hooke.
B adalah batas elastis dari kawat. Di atas titik ini, deformasi kawat adalah plastis. Jika tegangan baru dihilangkan dalam daerah deformasi plastis, misalnya di titik D, kawat logam tidak akan kembali ke bentuk semula, melainkan mengalami perubahan bentuk yang permanen (contohnya seperti kejadian melengkungnya klip kertas).
C adalah titik tekuk (yield point). Di atas titik ini hanya dibutuhkan tambahan gaya tarik kecil untuk menghasilkan pertambahan panjang yang besar. Tegangan yang paling besar yag dapat kita berikan tepat sesaat sebelum kawat patah disebut juga tegangan maksimum (ultyimate tensile stress). Sedangkan E adalah titik patah. Jika tegangan yang kita berikan mencapai titik E, maka kawat tersebut akan patah karenanya.
Dan untuk selanjutnya, bila kita memperhatikan grafik kembali dan memperhatikan dalam daerah OA, maka grafik berbentuk garis lurus. Dimana perbandingan antara tegangan dan regangan adalah konstan. Konstanta inilah yang disebut sebagai modulus elastis atau modulus young. Dengan demikian, modulus elastis suatu bahan (E) didefinisikan sebagai perbandingan antara tegangan dan regangan yang dialami bahan.



Modulus Elastisitas beberapa zat

Zat Modulus elastis
E (N/m²)
Besi 100 x 10
Baja 200 x 10
Batu bara 14 x 10
Marmer 50 x 10
Kayu 10 x 10
5.Tegangan Tarik, Tegangan Tekan, Tegangan Geser
Ada tiga jenis tegangan yang dikenal, yaitu tegangan tarik, tegangan tekan dan tegangan geser. Pada tegangan tekan, kedua ujung benda akan mendapatkan gaya yang sama besar dan berlawanan arah. Tapi, walau pemberian gaya dilakukan di ujung-ujung benda, seluruh benda akan mengalami peregangan karena tegangan yang diberikan tersebut.
Berbeda halnya dengan tegangan tarik, tegangan tekan berlawanan langsung dengan tegangan tarik. Materi yang diberi gaya bukannya ditarik, melainkan ditekan sehingga gaya-gaya akan bekerja di dalam benda, contohnya sepeti tiang-tiang pada kuil Yunani.
Tegangan yang ketiga adalah tegangan geser. Benda yang mengalami tegangan geser memiliki gaya-gaya yang sama dan berlawanan arah yang diberikan melintasi sisi-sisi yuang berlawanan. Misalkan sebuah buku atau batu-bata terpasang kuat dipermukaan. Meja memberikan gaya yang sama dan berlawanan arah sepanjang permukaan bawah. Walau dimensi benda tidak banyak berubah, bentuk benda berubah.

Elasitatas

energi potensial

Energi potensial adalah energi yang ditimbulkan oleh posisi relatif atau konfigurasi objek pada suatu sistem fisik. Bentuk energi ini memiliki potensi untuk mengubah keadaan objek-objek lain di sekitarnya, contohnya, konfigurasi atau gerakannya. Contoh sederhana energi ini adalah jika seseorang membawa suatu batu ke atas bukit dan meletakkannya di sana, batu tersebut akan mendapat energi potensial gravitasi. Jika kita meregangkan suatu karet gelang, kita dapat mengatakan bahwa karet gelang tersebu mendapatkan energi potensial elastik.

Berbagai jenis energi dapat dikelompokkan sebagai energi potensial. Setiap bentuk energi ini dihubungkan dengan suatu jenis gaya tertentu yang bekerja terhadap sifat fisik tertentu materi (seperti massa, muatan, elastisitas, suhu, dll). Energi potensial gravitasi dihubungkan dengan gaya gravitasi yang bekerja terhadap massa benda; energi potensial elastik terhadap gaya elastik (gaya elektromagnetik) yang bekerja terhadap elastisitas objek yang berubah bentuk; energi potensial elektrikal dengan gaya coulomb; gaya nuklir kuat atau lemah yang bekerja terhadap muatan elektrik pada objek; energi potensial kimia, dengan potensial kimia pada suatu konfigurasi atomik atau molekular tertentu yang bekerja terhadap struktur atomik atau molekular zat kimia yang membentuk objek; energi potensial termal dengan gaya elektromagnetik yang berhubungan dengan suhu objek.

energi potensial

ari Wikipedia bahasa Indonesia, ensiklopedia bebas

Langsung ke: navigasi, cari

Gravitasi bumi, salah satu gaya yang menimbulkan energi potensial.

Energi potensial adalah energi yang ditimbulkan oleh posisi relatif atau konfigurasi objek pada suatu sistem fisik. Bentuk energi ini memiliki potensi untuk mengubah keadaan objek-objek lain di sekitarnya, contohnya, konfigurasi atau gerakannya. Contoh sederhana energi ini adalah jika seseorang membawa suatu batu ke atas bukit dan meletakkannya di sana, batu tersebut akan mendapat energi potensial gravitasi. Jika kita meregangkan suatu karet gelang, kita dapat mengatakan bahwa karet gelang tersebu mendapatkan energi potensial elastik.

Berbagai jenis energi dapat dikelompokkan sebagai energi potensial. Setiap bentuk energi ini dihubungkan dengan suatu jenis gaya tertentu yang bekerja terhadap sifat fisik tertentu materi (seperti massa, muatan, elastisitas, suhu, dll). Energi potensial gravitasi dihubungkan dengan gaya gravitasi yang bekerja terhadap massa benda; energi potensial elastik terhadap gaya elastik (gaya elektromagnetik) yang bekerja terhadap elastisitas objek yang berubah bentuk; energi potensial elektrikal dengan gaya coulomb; gaya nuklir kuat atau lemah yang bekerja terhadap muatan elektrik pada objek; energi potensial kimia, dengan potensial kimia pada suatu konfigurasi atomik atau molekular tertentu yang bekerja terhadap struktur atomik atau molekular zat kimia yang membentuk objek; energi potensial termal dengan gaya elektromagnetik yang berhubungan dengan suhu objek.

Artikel bertopik fisika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengemba

kuat medan magnet

Medan Magnet di Sekitar Kawat Lurus

Besarnya medan Magnet disekitar kawat lurus panjang berarus listrik. Dipengaruhi oleh besarnya kuat arus listrik dan jarak titik tinjauan terhadap kawat. Semakin besar kuat arus semakin besar kuat medan magnetnya, semakin jauh jaraknya terhadap kawat semakin kecil kuat medan magnetnya.

Berdasarkan perumusan matematik oleh Biot-Savart maka besarnya kuat medan magnet disekitar kawat berarus listrik dirumuskan dengan :

• B = Medan magnet dalam tesla ( T )
• μo = permeabilitas ruang hampa =
• I = Kuat arus listrik dalam ampere ( A )
• a = jarak titik P dari kawat dalam meter (m)

Arah medan magnet menggunakan aturan tangan kanan

Medan magnet adalah besaran vector, sehingga apabila suatu titik dipengaruhi oleh beberapa medan magnet maka di dalam perhitungannya menggunakan operasi vektor.
Berikut ditampilkan beberapa gambar yang menunnjukkan arah arus dan arah medan magnet.
Arah medan magnet didaerah titik P ( diatas kawat berarus listrik ) menembus bidang menjauhi pengamat sedang didaerah titik Q dibawah kawat berarus listrik menembus bidang mendekati pengamat.
Tanda titik menunjukkan arah medan menembus bidang mendekati pengamat.
Tanda silang menunjukkan arah medan menembus bidang menjauhi pengamat.
Tanda anak panah biru menunjukkan arah arus listrik.

Pada sumbu koordinat x, y, z kawat berarus listrik berada pada bidang xoz dan bersilangan dengan sb. Z negative. Arah arus listrik searah dengan sumbu x positif.
Jarak antara kawat I dengan titik pusat koordinat (O) adalah a maka besarnya medan magnet dititik (O) tersebut searah dengan sumbu y negative.

Keterangan gambar:
I = arus listrik
B = medan magnet
Tanda panah biru menunjukkan arah arus llistrik

Contoh :

Sebuah kawat lurus panjang dialiri arus 5 miliampere berada diruang hampa . Tentukan besarnya induksi magnetic pada titik yang berada sejauh 10 cm disebelah kanan kawat, bila kawat vertikal ?

Jawab :
Diketahui : I = 5 miliampere = 5 . 10 ^{– 3} Ampere
a = 10 cm = 0,1 meter
Ditanya : B = ………….?
Dijawab :

Sebuah kawat berada pada sumbu x dialiri arus listrik sebesar 2 A searah dengan sumbu x positif . Tentukan besar dan arah medan magnet dititik P yang berada pada sumbu y berjarak 4 cm dari pusat koordinat 0 ( lihat gambar) ?

Dijawab :
Dketahui : I = 2 A
a = 4 . 10 – 2 m
Ditanya : Besar dan arah B ….. ?
Dijawab :

hukum gravitasi

Gravitasi adalah gaya tarik-menarik yang terjadi antara semua partikel yang mempunyai massa di alam semesta. Fisika modern mendeskripsikan gravitasi menggunakan Teori Relativitas Umum dari Einstein, namun hukum gravitasi universal Newton yang lebih sederhana merupakan hampiran yang cukup akurat dalam kebanyakan kasus.

Sebagai contoh, bumi yang memiliki massa yang sangat besar menghasilkan gaya gravitasi yang sangat besar untuk menarik benda-benda di sekitarnya, termasuk makhluk hidup, dan benda-benda yang ada di bumi. Gaya gravitasi ini juga menarik benda-benda yang ada diluar angkasa, seperti bulan, meteor, dan benda angkasa lainnya, termasuk satelit buatan manusia.

Beberapa teori yang belum dapat dibuktikan menyebutkan bahwa gaya gravitasi timbul karena adanya partikel gravitron dalam setiap atom.

[sunting] Hukum Gravitasi Universal Newton

Hukum gravitasi universal Newton dirumuskan sebagai berikut:

Setiap massa titik menarik semua massa titik lainnya dengan gaya segaris dengan garis yang menghubungkan kedua titik. Besar gaya tersebut berbanding lurus dengan perkalian kedua massa tersebut dan berbanding terbalik dengan kuadrat jarak antara kedua massa titik tersebut.

F adalah besar dari gaya gravitasi antara kedua massa titik tersebut

G adalah konstanta gravitasi

m₁ adalah besar massa titik pertama

m₂ adalah besar massa titik kedua

r adalah jarak antara kedua massa titik

Dalam sistem Internasional, F diukur dalam newton (N), m₁ dan m₂ dalam kilograms (kg), r dalam meter (m), dsn konstanta G kira-kira sama dengan 6,67 × 10⁻¹¹ N m² kg⁻².

Dari persamaan ini dapat diturunkan persamaan untuk menghitung Berat. Berat suatu benda adalah hasil kali massa benda tersebut dengan percepatan gravitasi bumi. Persamaan tersebut dapat dituliskan sebagai berikut: W = mg. W adalah gaya berat benda tersebut, m adalah massa dan g adalah percepatan gravitasi. Percepatan gravitasi ini berbeda-beda dari satu tempat ke tempat lain.

gaya gesek

Gaya gesek adalah gaya yang bekerja pada benda dan arahnya selalu melawan arah gerak benda. Gaya gesek hanya akan bekerja pada benda jika ada gaya luar yang bekerja pada benda tersebut.

BENDA DIAM	AKAN BERGERAK	MULAI BERGERAK

f_s = gaya gesek statis
m_s = koefisien gesek statis
f_k = gaya gesek kinetis
m_k = koefisien gesek kinetis
P = Resultan gaya reaksi yang mengimbangi gaya aksi F dan W

Nilai f_s antara nol sampai maksimum (nilai f_s = 0 jika tidak ada gaya luar F yang bekerja pada benda, dan nilai f_s mencapai maksimum pada saat benda akan bergerak). f_s maksimum ini tergantung pada sifat permukaan benda dan lantai yang bersinggungan serta tergantung pada gaya normal.

Kinematika gerak

Kinematika adalah ilmu yang membahas tentang gerak tanpa meninjau penyebab terjadinjya gerak. Setiap Hari kita berangkat dari rumah ke tempat kerja atau ke sekolah, tanpa kita sadari kita telah melakukan pergerakan atau perpindahan kedudukan dari rumah ke kantor atau sekolah. Hal yang demikian dikatakan kita melakukan perpindahan/bergerak.

Kinematika gerak

Kinematika adalah ilmu yang membahas tentang gerak tanpa meninjau penyebab terjadinjya gerak. Setiap Hari kita berangkat dari rumah ke tempat kerja atau ke sekolah, tanpa kita sadari kita telah melakukan pergerakan atau perpindahan kedudukan dari rumah ke kantor atau sekolah. Hal yang demikian dikatakan kita melakukan perpindahan/bergerak.

hukum keppler

Di dalam astronomi, tiga Hukum Gerakan Planet Kepler adalah

• Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya.
• Luas daerah yang disapu pada selang waktu yang sama akan selalu sama.
• Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari.

Ketiga hukum diatas ditemukan oleh ahli matematika and astronomi jerman Johannes Kepler (1571–1630), yang menjelaskan gerakan planet di dalam tata surya. Hukum diatas menjabarkan gerakan dua benda yang saling mengorbit.

Karya Kepler didasari oleh data observasi Tycho Brahe, yang diterbitkannya sebagai 'Rudolphine tables'. Sekitar tahun 1605 Kepler menyimpulkan bahwa data posisi planet hasil observasi Brahe mengikuti rumusan matematika cukup sederhana yang tercantum diatas.

Hukum Kepler mempertanyakan kebenaran astronomi dan fisika warisan zaman Aristoteles dan Ptolemaeus. Ungkapan Kepler bahwa Bumi beredear sekeliling, berbentuk elips dan bukannya epicycle, dan membuktikan bahwa kecepatan gerak planet bervariasi, merubah astronomi dan fisika. Hampir seabad kemudian Isaac Newton mendeduksi Hukum Kepler dari rumusan hukum karyanya, hukum gerak dan hukum gravitasi Newton, dengan menggunakan Euclidean geometry klasik.

Pada era modern, hukum kepler digunakan untuk aproximasi orbit satelit dan benda-benda yang mengorbit matahari. Yang semuanya belum ditemukan pada saat Kepler hidup. (contoh: planet luar dan asteroid) Hukum ini kemudian diaplikasikan untuk semua benda kecil yang mengorbit benda lain yang jauh lebih besar, walaupun beberapa aspek seperti gesekan atmosfer (contoh: gerakan di orbit rendah), atau relativitas (contoh: prosesi preihelion merkurius), dan keberadaan benda lainnya dapat membuat hasil hitungan tidak akurat dalam berbagai keperluan.

Daftar isi [sembunyikan] 1 Introduksi Tiga Hukum Kepler 1.1 Secara Umum 1.2 Hukum Pertama 1.3 Hukum Kedua 1.4 Hukum Ketiga 2 Sejarah 2.1 Pustaka 2.2 Pranala luar

[sunting] Introduksi Tiga Hukum Kepler

[sunting] Secara Umum

Hukum hukum ini menjabarkan gerakan dua badan yang mengorbit satu sama lainnya. Masa dari kedua badan ini bisa hampir sama, sebagai contoh Charon—Pluto (~1:10), proporsi yang kecil, sebagain contol. Bulan—Bumi(~1:100), atau perbandingan proporsi yang besar, sebagai contoh Merkurius—Matahari (~1:10,000,000).

Dalam semua contoh diatas kedua badan mengorbit mengelilingi satu pusat masa, barycenter, tidak satupun berdiri secara sepenuhnya di atas fokus elips. Namun kedua orbit itu adalah elips dengan satu titik fokus di barycenter. Jika ratio masanya besar, sebagai contoh planet mengelilingi matahari, barycenternya terletak jauh di tengah obyek yang besar, dekat di titik masanya. Di dalam contoh ini, perlu digunakan instrumen presisi canggih untuk mendeteksi pemisahan barycenter dari titik masa benda yang lebih besar. Jadi, hukum Kepler pertama secara akurat menjabarkan orbit sebuah planet mengelilingi matahari.

Karena Kepler menulis hukumnya untuk aplikasi orbit planet dan matahari, dan tidak mengenal generalitas hukumnya, artikel wikini ini hanya akan mendiskusikan hukum diatas sehubingan dengan matahari dan planet-planetnya.

[sunting] Hukum Pertama

Figure 2: Hukum Kepler pertama menempatkan Matahari di satu titik fokus edaran elips.

"Setiap planet bergerak dengan lintasan elips, matahari berada di salah satu fokusnya."

Pada zaman Kepler, klaim diatas adalah radikal. Kepercayaan yang berlaku (terutama yang berbasis teori epicycle) adalah bahwa orbit harus didasari lingkaran sempurna. Pengamatan ini sangat penting pada saat itu karena mendukung pandangan alam semesta menurut Kopernikus. Ini tidak berarti ia kehilangan relevansi dalam konteks yang lebih modern.

Meski secara teknis elips yang tidak sama dengan lingkaran, tetapi sebagian besar planet planet mengikuti orbit yang bereksentrisitas rendah, jadi secara kasar bisa dibilang mengaproximasi lingkaran. Jadi, kalau ditilik dari observasi jalan edaran planet, tidak jelas kalau orbit sebuah planet adalah elips. Namun, dari bukti perhitungan Kepler, orbit orbit itu adalah elips, yang juga memeperbolehkan benda-benda angkasa yang jauh dari matahari untuk memiliki orbit elips. Benda-benda angkasa ini tentunya sudah banyak dicatat oleh ahli astronomi, seperti komet dan asteroid. Sebagai contoh Pluto, yang diobservasi pada akhir tahun 1930, terutama terlambat diketemukan karena bentuk orbitnya yang sangat elipse dan kecil ukurannya.

[sunting] Hukum Kedua

Figure 3: Illustrasi hukum Kepler kedua. Bahwa Planet bergerak lebih cepat didekat matahari dan lambat dijarak yang jauh. Sehingga jumlah area adalah sama pada jangka waktu tertentu.

"Luas daerah yang disapu pada selang waktu yang sama akan selalu sama."

Secara matematis:

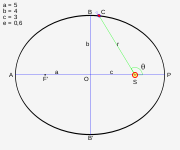
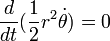
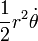dimana adalah "areal velocity".

[sunting] Hukum Ketiga

Planet yang terletak jauh dari matahari memiliki perioda orbit yang lebih panjang dari planet yang dekat letaknya. Hukum Kepelr ketiga menjabarkan hal tersebut secara kuantitativ.

"Perioda kuadrat suatu planet berbanding dengan pangkat tiga jarak rata-ratanya dari matahari."

Secara matematis:

dimana P adalah period orbit planet dan a adalah axis semimajor orbitnya.

Konstant proporsionalitasnya adalah semua sama untuk planet yang mengedar matahari.